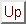Example 4: N-queens Problem

DJ can be used not only to build graphical user interfaces but also to solve constraint satisfaction problems in general. In this example, we show how to describe the N-queens problem and display the solutions graphically. Figure 3 shows a solution to the four queens problem.

The following shows the program:

       main class Queens {
             static public final int N = 4;
             component Rectangle squares[N][N];
             attribute int queens[N] in 0..N-1;
	   
             for (i in 0..N-1,j in 0..N-1) 
                   queens[i]!=j -> squares[i][j].fill==false;

             notattack(queens,N);
             grid(squares);
       }
       constraint notattack(int[] queens,int N){
             for (i in 0..N-2,j in i+1..N-1){
                   queens[i] != queens[j];
                   queens[i] != queens[j]+j-i;
                   queens[i] != queens[j]+i-j;
	       }
       }