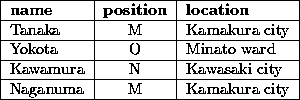
Table 1: An example of relation

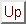

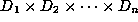 , where
, where
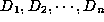 are domains. Each domain has a domain name
called an attribute which must be unique.
Domains must be finite sets in databases.
Table1 is an example of relation.
are domains. Each domain has a domain name
called an attribute which must be unique.
Domains must be finite sets in databases.
Table1 is an example of relation.

Table 1: An example of relation
Name, position and location are attributes under which there are
attribute values. A row of attribute values is called a tuple,
therefore, a relation is a set of tuples. And a relation is an ordered
set of attributes, i.e. 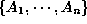 . A relation is sometimes
represented as
. A relation is sometimes
represented as 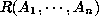 . Since relations have very simple
expressions, mathematical discussion of which is also simple.
Even though relations are kind of tables, all tables are not
recognized as relations. The following two conditions must be met for
a table to be a relation.
. Since relations have very simple
expressions, mathematical discussion of which is also simple.
Even though relations are kind of tables, all tables are not
recognized as relations. The following two conditions must be met for
a table to be a relation.
How can we represent the real world as relations. First, collect attributes of the world and make a table like table1. This flat table representation is a data structure of the relational data model. However, this relation has redundancy, for example in combination of position and location. Furthermore, if you change a combination of name and position, information of position and location might be meaningless. Thus, we normalize the original table(first normal form) taking into account dependencies.
A functional dependency can be defined when a collection of attribute
values 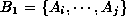 in relation
in relation 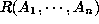 uniquely
decides another collection of attribute values
uniquely
decides another collection of attribute values
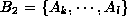 . In this case,
. In this case, 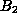 is functionally
dependent on
is functionally
dependent on 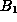 and expressed as
and expressed as 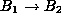 . Suppose
. Suppose
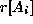 is an attribute value of
is an attribute value of 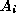 in a tuple r, the functional
dependency means as follows for arbitrary tuples
in a tuple r, the functional
dependency means as follows for arbitrary tuples 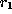 and
and 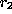 .
.
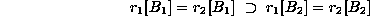
In table1, there are two functional dependencies, that are
name position and position
position and position location.
If Yokota changes his position, the location of which have to be also
changed. Then the information that position O is in Minato ward will
get lost. That is why we devide table1 into table2.
Generally, we should devide a table into tables in which functional
dependencies are all on their keys. This type of relation is in third
normal form. The decomposition based on functional dependencies includes
second normal form which is different from third normal form in terms
of kind of functional dependencies. Third normal form not only
prevents above mentioned loss of information but also makes tables
simpler excluding repetitive pairs of position and location as you can
see in table2. In other words data redundancy decreases, so
you will have to update only one tuple if the location of position O
changes.
location.
If Yokota changes his position, the location of which have to be also
changed. Then the information that position O is in Minato ward will
get lost. That is why we devide table1 into table2.
Generally, we should devide a table into tables in which functional
dependencies are all on their keys. This type of relation is in third
normal form. The decomposition based on functional dependencies includes
second normal form which is different from third normal form in terms
of kind of functional dependencies. Third normal form not only
prevents above mentioned loss of information but also makes tables
simpler excluding repetitive pairs of position and location as you can
see in table2. In other words data redundancy decreases, so
you will have to update only one tuple if the location of position O
changes.
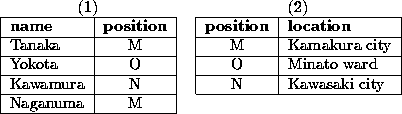
Table 2: Decomposition by functional dependencies
Normalization of relations are done not only by functional dependencies but by multivalued dependencies. Let's look at table 3. This relation consists of three attributes of name, hobby and club. It has no functional dependency.

Table 3: Relation including multivalued dependencies
If you devide table3 into table4, redundancy
decreases. Both hobby and club have plural values against name. This
property is called multivalued dependency. In this case the
multivalued dependencies are expressed as
name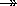 hobby and
name
hobby and
name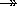 club, which means that the
original relation can be decomposed into two relations of
club, which means that the
original relation can be decomposed into two relations of
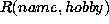 and
and 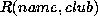 . It is obvious that even if decomposed
relations are joined to a relation, no information loss occurs.
. It is obvious that even if decomposed
relations are joined to a relation, no information loss occurs.

Table 4: Decomposition by multivalued dependencies
Dependencies other than functional and multivalued dependencies are considered. The most important thing here is that joined relations have the same amount of information as decomposed relations. Muximum relationship among decomposable attributes are called join dependency.
Next, let's think about data manipulations of relations. In the relational model there are relational algebra which centers on set operations and relational calculus which uses first-order predicate calculus.
Relational algebra includes the following five operations.
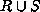 is a set
union of tuples in R and those in S.
is a set
union of tuples in R and those in S.
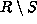 is
a set of tuples which belong to R and do not belong to S.
is
a set of tuples which belong to R and do not belong to S.
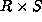 is
is
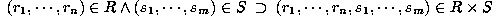
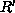 which satisfies a conditional
logical formula C out of a relation R is called selection
from R by C. The expression of the selection is
which satisfies a conditional
logical formula C out of a relation R is called selection
from R by C. The expression of the selection is
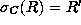 . C is a logical formula composed of
attribute names, attribute values, arithmetic operators,
comparison operatiors and logical operators. The evaluation of
C is done by substituting attribute values of actual tuples
for attibute names in C.
. C is a logical formula composed of
attribute names, attribute values, arithmetic operators,
comparison operatiors and logical operators. The evaluation of
C is done by substituting attribute values of actual tuples
for attibute names in C.
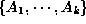 from relation
R. The operation is expressed as
from relation
R. The operation is expressed as 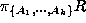 . For example, table3 is projected by name and
hobby to make table4(1).
. For example, table3 is projected by name and
hobby to make table4(1).
The above basic operations are combined to define the following operations.
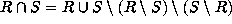 .
.
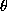 -Join
-Join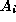 and
and
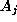 are attributes in R and S respectively. The
are attributes in R and S respectively. The
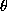 -join of R and S on
-join of R and S on 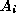 and
and 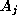 is a relation
denoted by
is a relation
denoted by 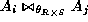 . Here,
. Here,
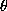 is an arithmetic comparison operator and if it is an
equal, the operation is called equi-join. Furthermore, if the
only one of the same attributes is left and the other is
removed from the equi-joined relation, the operation is called
natural-join.
is an arithmetic comparison operator and if it is an
equal, the operation is called equi-join. Furthermore, if the
only one of the same attributes is left and the other is
removed from the equi-joined relation, the operation is called
natural-join.
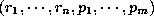 and
and 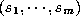 .
The division
.
The division 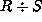 is an operation to find
is an operation to find
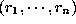 for which
for which 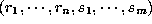 are included in tuples of R for all
are included in tuples of R for all 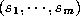 .
It is obvious that
.
It is obvious that 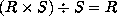 .
.
Those mentiond operations including the first five basic ones and
the latter three composites are so-called relational algebra.
On the other hand, relational calculus is generaly a set of tuples
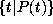 which satisfies a logical formula
which satisfies a logical formula 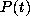 where an
argument t is a tuple variable. It has been proved that all the
relational algebraic operations can be translated in relational
calculus and if the scope of tuple variables are specified,
they are equivalent.
where an
argument t is a tuple variable. It has been proved that all the
relational algebraic operations can be translated in relational
calculus and if the scope of tuple variables are specified,
they are equivalent.