4.外部講師講演概要
4.1 分子生物情報分野での知的な情報処理(講師:三菱電機 田中秀俊氏)
分子生物情報分野で特に求められている情報処理技術は、さまざまなシミュレータの構築技術であろう。分子生物情報学の目指す目標のひとつは、染色体からの遺伝子発現を予測し、その遺伝子からタンパク質のアミノ酸配列を算出してその立体構造や機能を予測し、その機能がどのように他の機能と相互作用して細胞活動が行われるかを予測するという、いわゆるセントラルドグマから細胞活動までのトータルなシミュレーションにある。そのための要素技術として、例えば核酸配列やアミノ酸配列の解析に自然言語解析の技術、立体構造の予測や機能の予測には学習の技術、機能ネットワークの蓄積には知識表現の技術が役に立つと考えられる。本章では分子生物という分野で需要のあるシミュレーションを列挙して、そこでどのようにこれら知的情報処理技術が役に立っているか、もしくは今後役に立つようになってきそうかについて、簡単に紹介する。
4.1.1 遺伝子発現のシミュレータ
4.1.1.1 遺伝子発現領域の予測
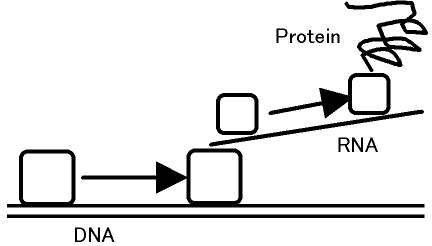
人間の遺伝情報、すなわち人間の細胞がどのようなタンパク質から構成されるかという情報は、染色体の核酸の並び(核酸配列と呼ばれる)で表される。遺伝情報からタンパク質が作られるときには、まずその核酸配列に特定の物体(
RNAポリメラーゼなど)がとりつき、配列上を一定区間滑って離れる。そのときこの物体は核酸配列をテープとする一種のチューリングマシンの役割を果たして、別の核酸配列を生成する。その核酸配列には、真核生物の場合さらに中に含まれたゴミ(イントロン)を捨てるという処理が挟まった後、また別のチューリングマシン(リボソームなど)がとりついて、配列上を一定区間滑って離れ、そのときアミノ酸配列を生成する。この生成されたアミノ酸配列が、折り畳まってある立体構造をとり、場合によっては複数の配列が合わさって、タンパク質になる。(図4.1-1)チューリングマシンは、ある特定の部分配列を見つけるとそこにとりつき、また別のある特定の部分配列の箇所で離れるようになっている。チューリングマシンが核酸配列やアミノ酸配列を生成する規則は単純で、前者の場合は1対1の変換であり、後者は特定の開始文字列(開始コドン)から終了文字列(終止コドン)までの、核酸3文字(3塩基)からアミノ酸1文字(1残基)への変換である。チューリングマシンのとりつく箇所と離れる箇所の部分配列を発見し、その間で開始コドンから終止コドンまで3文字ずつ納まる一連の読み枠が見つかれば、アミノ酸配列生成部分の先頭と末尾、すなわち遺伝子発現領域が判明する。これにより、大量に解読された核酸配列を機械にかけて、どこが遺伝子発現領域なのかを精度よく予測できるようになる。
さらに、チューリングマシンがとりつく部分の周辺には別の物体(制御因子)がとりついて、チューリングマシンの結合のしやすさを加減したり、単に障害物となって結合を抑止したりする。この物体も、ある特定の部分配列を見つけてとりつくようになっている。制御因子の存在は後述の遺伝子発現シミュレータでも重要なポイントになるが、発現領域予測においても重要で、制御因子のとりつく配列のあるなしを考慮した予測によって精度向上が図られるようである。

図4.1-1 遺伝子の発現(略図)
4.1.1.2 隠れマルコフモデルによる発現領域予測
核酸配列は
ACGTの4文字種で表現されるので、このような特定部分配列も4文字種からなる文字列で表される。この文字列の発見には、マルチプルアライメントと呼ばれる手法が用いられる。これは、例えば「とりつき」の発生しそうな部分を実験によって複数入手した後、ギャップを適当に入れてそれらを並べることによって、共通な文字列パターンを発見する手法である。図4.1-2に簡単な例を示す。図では、ACGTの文字列を縦に揃えることにより、AATAAAという共通のパターンが見えている。これをかつては当然人間が目で見て並べていたが、動的計画法を用いて計算機で2つの文字列を並べる手法が確立されて以後、計算機によるマルチプルアライメントがさかんに研究されるようになった。以下はDNAでなくRNA配列やタンパク質のアミノ酸配列を対象にしたものだが、3つ以上の文字列を並列計算機を用いて並べる技術[1]、2つのマルチプルアライメント結果を並べる技術[2]、A*アルゴリズムを用いる技術[3,4]などがその代表例である。
![]()
図4.1-2 マルチプルアライメント
このマルチプルアライメントが、隠れマルコフモデルと同等であることが示されたことをきっかけとして、隠れマルコフモデルによる共通配列解析やマルチプルアライメントの研究がさかんになった[5]。現状で入手可能な発現領域予測ツールの中にも、隠れマルコフモデルをベースとしたものがあり、優秀な成績をあげているようである[6,7,8]。隠れマルコフモデルとは、ある確率分布に従って文字を出力する状態をいくつか用意し、その状態間の遷移によって文字列を表現するモデルである。図4.1-3はマルチプルアライメント用の隠れマルコフモデルのモデル形状の例である。図中、丸や四角は状態を、線は左から右への向きの状態間遷移を表している、一致状態と削除状態は自己遷移ループを持つが、それは省略して記述している。このモデルでは、マルチプルアライメントにおけるギャップの挿入が削除状態と挿入状態とで表現され、それは図では四角で表現されている部分である。一致状態が共通パターンを表わす。
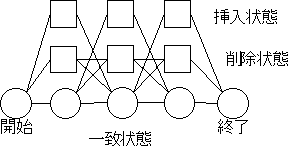
図4.1-3 マルチプルアライメント用隠れマルコフモデルの例
4.1.1.3 確率的文法規則を用いた発現領域予測
先頭と末尾だけでなく、この物体のとりつき部分や、イントロンと呼ばれる遺伝子内のゴミ部分についても表現を試みたりすると、部分配列同士の相互の関係、つまり遺伝子の文法構造を考えるようになる。そこで仮定する文法クラスとしては、扱いやすい確率的文脈自由文法で納まるようにする研究がなされるようである[
9]。このクラスに納まらない代表例としては、x_y_x_yで表わされるようなシュードノットと呼ばれる文法構造(図4.1-4参照)や、xn yn zn のような所定数の反復のある文法構造などがある[10]。
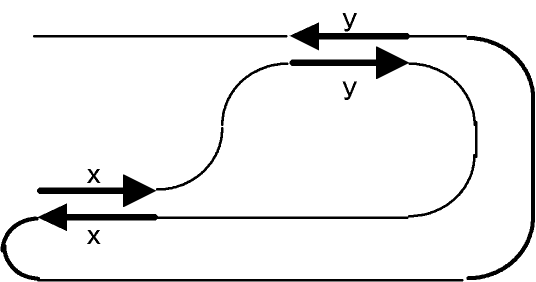
図4.1-4 シュードノット構造
4.1.2 タンパク質折り畳みシミュレータ
4.1.2.1 タンパク質の立体構造予測
近年、核酸配列の解読が簡易化し、そのため遺伝子の核酸配列と、そこからほぼ一意に求まるアミノ酸配列の公開データが爆発的に増えている。しかし核酸配列に対応するアミノ酸配列が求まっても、その組成を持つタンパク質の機能はそこからは直接にはなかなか分からない。ただしタンパク質の機能は他のどのような物質と接触や結合が起こるかによってほとんどが決定されるので、立体構造がわかればその機能のかなりの部分が予測できると信じられている。よって、ヒモ状のアミノ酸配列が三次元的に折り畳まった形状を予測することが重要視されており、予測を競う国際的なコンテスト
CASP[11]も隔年開催されている。このシミュレータの実現方法は大きく2通りあり、ひとつは分子動力学法によって力学モデルで算出してしまう方法、もうひとつは、配列が類似している構造既知タンパク質を参照する類似検索法である。後者は、かつては類似した配列断片を捜すだけの二次構造予測が主だったが、最近は3D−1D法やスレッディングと呼ばれる構造全体の類似検索が注目されている。
4.1.2.2 分子動力学法による予測
分子動力学法によるタンパク質折り畳みで取り扱う問題は、タンパク質分子だけでなく溶液分子を含めた多体問題である。よって、電気力や万有引力など各種の相互作用を見積もりながら、微小時間毎に分子の位置を計算していくアプローチがとられる。この方法をとると、現在最高水準の計算機でも数か月かけて数ナノ秒分の折り畳み計算ができる程度と言われ、数ミリ秒かかる折り畳みのシミュレーションには少なくとも百万倍高速な計算機が要求される。これは大規模並列計算機の応用分野として注目されており、例えばバーンズハットモデルと呼ばれる宇宙科学の分野で用いられる方法を応用した効率的計算法に関する研究などが著名である[
12]。
4.1.2.3 類似検索による二次構造予測
二次構造予測は、構造と配列が既知のタンパク質を集めたデータベースにおいて、部分構造に二次構造と総称されるラベルが付されていて、そのラベルを構造未知の配列に正しく貼る予測である。二次構造のラベルでよく用いられるのはα、β、Lであり、それぞれ左巻き螺旋構造、シート構造やバレル構造、右巻き螺旋構造を表す。この場合はどれでもないものは無ラベルである。図
4.1-5に示したタンパク質のリボン表示の例では、左上と右下の螺旋構造がα構造、中央の紐の往復がβ構造である。これらのラベルは、観察結果を大まかに分類する用途には特に支障がないが、構造予測をしたい場合にはおおまか過ぎるので、構造予測のために二次構造を細かく分類する研究も行われている[13,14]。二次構造予測には、
PDBのような生のタンパク質立体構造データベースではなく、そのデータベースを加工した二次データベースであるタンパク質モチーフデータベース、例えばProSiteがよく用いられる[15]。これは特定の機能や構造を持つタンパク質にどのような配列パターンが含まれているかという情報をまとめたものである。昔はこの配列パターンを正規表現類似の形式で記録していた。例えばCytochromeCのモチーフ(の一部)はCxxCH という形式で表現される。これは、CytochromeCのアミノ酸配列には共通に適当な2残基挟んでCysteineが2つ含まれ、その直後にHistidineがくるようなパターンが存在することを表している。しかし、xxの部分にも弱い確率的傾向があるので、それも表現しようとして、近年はマルチプルアライメントを数値化したプロファイルと呼ばれる表現方法を併用するようになった。このプロファイルは、隠れマルコフモデルと基本的には同じ表現形式と言える。二次構造予測は
ProSiteのモチーフに自分で発見したモチーフを加え、未知配列とそのモチーフ群を突き合わせて、未知配列の断片とモチーフとの類似を見つけ出すことで行うのが一般的である。モチーフデータベースを隠れマルコフモデルの形式に変換して、生のデータからの学習の手間を軽減し精度を向上させる方法も考えられ、実際に核酸配列における遺伝子発現領域予測ではそのような研究がある[16]。二次構造は、当てやすいα構造で8割、比較的遠い残基間での相互作用を伴うためやや見つけにくいβ構造でも7割弱、全体でも7割弱くらい当たるというのが世間相場らしい。二次構造予測での大きな問題は、データベースの品質にある。同じ配列に対し、α構造に
10票、β構造に2票入ったからといって、単純な多数決でα構造と決めてしまうのではなく、α構造に入った10票がどのような偏りを持った10票なのかを調査しなければならない。極端な例を挙げるなら、CytochromeCしかない偏ったデータベースからモチーフを抽出してそれをHemoglobinに適用しても、いい予測は得られないだろう。
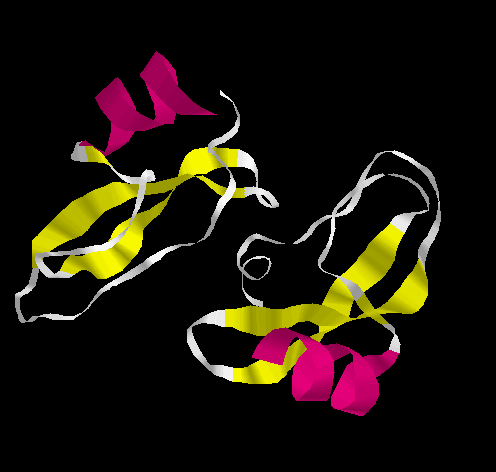
図4.1-5 リボン表示によるタンパク質の例
4.1.2.4 類似検索による立体構造予測
データベースの既知構造に構造未知の配列を次々にあてはめてみて、最も良くあてはまる物を求める3D−1D法という立体構造予測法が最近の注目を集めている。構造への配列のあてはめには、動的計画法などマルチプルアライメントとほぼ同じ手法が用いられる[
17]。3D−1D法の問題は、二次構造予測同様、データベースの偏りの解消にある。特に既知構造1本対未知構造1本であてはめると偏りが強いため、既知構造側に類似した複数本を用意しておき、未知構造側も配列データベースから類似配列を検索して複数本にして、両者をマルチプルアライメントするような方法をとると、偏りがある程度解消されて予測精度が向上するようである。この方式はちょうど、立体構造上は近隣で配列上は遠距離にあるような、従来のモチーフでは捕らえにくかった残基間の関係も隠れマルコフモデルのような確率過程的な表現に含めたことに相当すると考えられる。この点も3D−1D法が優秀な理由のひとつと見られる。
4.1.3 ドッキングシミュレータ
タンパク質の機能は、他のどのような物質と接触や結合が起こるかによってほとんどが決定されるので、立体構造がわかればその機能のかなりの部分が予測できると信じられている。生体内には特定のタンパク質と結合する性質を持つリガンドと総称される物質群があり、主に情報伝達に用いられているらしい。ドッキングシミュレータは、そのような物質間の結合や接触が起こるかどうかを判定し、その形態を予測し、それによって例えばタンパク質のリガンドを検索したり、ある物質がリガンドかどうかを判定したりする機能を提供するものである。
このシミュレータの実現方式には、まず前章で紹介した分子動力学による方法が挙げられる。しかしナノ秒の範囲までしか実用時間内に計算できないという現状では、結合寸前の状態を人為的に作り上げ、そこから結合がどう起こるかを観察するくらいにしか使えないようである。これも折り畳みシミュレーション同様に数百万倍の性能向上が期待される。一方、特徴を抽出して経験的な判定や予測を行う方法もある。例えばタンパク質の凹凸を解析し、最大マッチングを探索する問題に帰着するアプローチが考えられ、これに関しては「数理形態学」の技術を適用した凹凸解析の研究[
18]、遺伝的アルゴリズムを用いてドッキングの探索を行う分子設計支援ソフトウェア[19,20]などがある。
4.1.4 生化学反応系シミュレータ
4.1.4.1 生化学反応データベースの問合せ処理
現在
WWW上で提供されている生化学反応データベースは数多いが、通常、情報の追加や修正はページ製作者が責任を持って慎重に行っているようである[21]。一方、生体内のさまざまな物質間の生化学反応の知識は、日夜増え続けている。そこで核酸配列の公共データベースGenBankやタンパク質の立体構造データベースPDBのように、実験結果を受け付けて拡大する公共データベースを用意したいという要求が発生する。生化学反応データベースの公共化に必要なのは、反応の要素としての物質の表現に関する技術と、反応シミュレータの構築技術であると考えられる。
4.1.4.2 物質や反応の表現方法
公共生化学データベースにおける物質や反応の表現方法については、いくつかの選択肢が考えられる。物質は名前で表現するか、それとも原子のネットワーク(化学構造)で表現するか、反応は関わる物質で表現するのか、識別子を別途つけるか。どれを選択するにしても、現状ではあまり簡単な表現にはなりそうになく、公共データベースの運用や普及の妨げになっていることは疑いない。
反応とは、教科書的には「ある物質の
OHと別の物質のHと、酵素と適当なエネルギーとを与えると、そこをH2Oにするとともに両物質を結合させ、しかるべきエネルギーを発生する」などという格好をしている。この場合「OHを持つ物質」「Hを持つ物質」などがデータベース上での物質の表現になる。このデータベースに基づいて、実際の物質の名称が与えられた時にこの反応に該当するかどうかを判断するには、その名称の物質がOHを持つかどうか、Hを持つかどうかといった知識を蓄えたデータベースが別途必要になる。一方、実際の物質の分子構造が与えられた時にこの反応に該当するかどうかを判断するには、グラフの部分マッチングの仕組みが必要になる。また、このような教科書的な反応記述ではなく、実験結果がデータベースに蓄積されている場合を考える。例えばカルボン酸(R
1−COOH)とアルコール(R2−OH)がエステル(R1COOR2)と水になるという反応が、さまざまなカルボン酸とアルコールの組合せについてデータベースに多数蓄積されており、そこにR1部分の複雑なカルボン酸の化学構造が示され、関わりそうな反応について問合せがあったとする。この問合せに答えたいなら、化学構造の類似性判定、つまりグラフ間の類似判定の仕組みが必要になる。公共生化学反応データベースを構築する場合、教科書的な反応はできる限り事前に格納された上に、多数から寄せられた実験結果がいくつも格納された形で運用される。実験結果を適宜集めては教科書的な知識を付与する必要もある。修正を受け付ける必要も生じる。以上の点を考慮すると、削除や更新を受け付けず単調にデータが蓄積し、各データ(トランザクション)には最新データを得るためのタイムスタンプと信頼性を示すためのデータ登録者情報とを持つ、データウェアハウス的な構造が適していると思われる。
4.1.4.3 反応間の関係の表現方法
ある実験結果を説明するのがひとつの反応だけという例はむしろ稀で、ひとつの実験結果が一続きの反応を示唆することの方が多いだろう。また、複数の反応が関わって一続きの大きな反応を構成することもしばしばある。例えば平衡は向きの違う2つの反応の集まりと見なせる。その平衡がいくつか連なってエネルギーの流れや電子の流れを生み出すこともある。このような反応間の連結関係や概念的上下関係の記述方法が、またひとつの問題となる。
タンパク質の機能のデータベースを構築する試みとして、判明している部分的な代謝反応を演繹オブジェクト指向言語の枠組みで知識ベースに蓄積していき、質問に応じて部分的な代謝反応ネットワークを構築して提供する研究がかつて行われた[
22]。そこでは物質間の関係と反応間の関係を同じ枠組みで記述できるようにしており、ある反応がその全体のネットワークの中でどこに位置するかを動的に提示する機能の実現を目標としていた。しかし実際の構築はそのごく一部のプロトタイプに留まった。
4.1.4.4 生化学反応シミュレータの自動構築
生化学反応データベースの問合せは、反応に関する質問か、物質の増減に関する質問だろう。前者は従来のデータベースや知識ベースの問合せ処理で対応可能だが、後者についてはシミュレータを構築する処理が必要になる。つまり、ある物質を増やしたり減らしたりしたら別の特定物質の量は一定時間内にどう変化するのか、という問合せに応じて、物質間の反応関係やそれら反応間の関係を記述したデータベースに基づき、2つの物質をつなぐ反応にはどのようなものがあるかを検索し、シミュレータを構築するのである。データベース上に問合せに応じて構築されるシミュレータ、あるいは未来に関する質問に答えるデータベースと言ってもよいが、これはデータベースの傾向に関する質問に答える技術、つまりデータマイニング[
23]と呼ばれている技術の一種、もしくはその延長線上にある技術と言えるのかもしれない。
4.1.5 遺伝子発現系シミュレータ
染色体には多数の遺伝子が含まれている。各遺伝子にはその遺伝子の発現を制御する部分が付随しており、その部分の配列の差が発現の量に反映される。この部分配列による発現量制御は、制御因子と呼ばれる別のタンパク質が当該配列に結合することで行われることが多い。そのタンパク質の発現量制御には、また別のタンパク質が関係する。このように、遺伝子の発現には連鎖反応的な関係が存在する。よって前章の生化学反応系シミュレータ同様、部分的な知見を蓄積する公共遺伝子発現データベースの需要があり、遺伝子発現シミュレータの構築の需要がある。現在
WWW上で提供されている遺伝子発現データベースは、生化学反応データベース同様、情報の追加や修正をページ製作者以外に開放している例は見当たらない[21]。遺伝子発現ネットワークはノードとなる遺伝子が文字列などによって比較的特定が容易であり、この点は生化学反応の表現に比べてやや扱いやすいと言えるが、それ以外の技術課題は生化学反応と同じと考えられる。
4.1.6 細胞活動シミュレータ
生化学反応系や遺伝子発現系といった機能のネットワークを中心に必要最小限の系を構築し、細胞の代謝や分裂に関するシミュレーションを行う研究が、慶応大学冨田研の
E-Cellプロジェクトにて行われている[24]。このプロジェクトは、単細胞バクテリアの生化学反応を丸ごとシミュレーションするもので、1997年には127個の遺伝子を持った仮想細胞モデルを構築し、ISMB98にも出展して賞を受けている。
4.1.7 分子生物情報分野における知的情報処理の今後
当該分野では、ゲノムの完読という「作業」がいくつかの生物で完了し、研究者は本来の「研究」である遺伝子やタンパク質の機能の探求に着手し始めている。当面注目されるのは、遺伝子発現領域の予測などに活用できる学習の技術、特に分類の技術で、それに続くのはシミュレータ構築に活用できる技術、回帰分析的な学習や関数最適化の技術だと考えている。一方で、大きな注目はされないかもしれないが必要不可欠なものとして、生化学反応の公共データベースを構築するための、おそらくさまざまな点の標準化と、その裏付けとなる知識表現やオントロジーの技術が重要になると考えている。
<参考文献>
[
1] 広沢他. 3次元ダイナミックプログラミングを活用した蛋白質のアライメントシステム. Genome Informatics Workshop II. pp.120-123. (1991).[
2] Berger, M.P. and Munson, P.J. A Novel Randomized Iterative Strategy for Aligning Multiple Protein Sequences. CABIOS 7(4):479-484.[
3] 十時他. アミノ酸配列のマルチプルアラインメントにおける反復改善過程の並列化とA*アルゴリズムの適用. 情報処理学会研究会論文誌. Vol.40 MPS No.2. (1999).[
4] Kobayashi, H., and Imai, H. Improvement of the A* Algorithm for Multiple Sequence Alignment. Genome Informatics 1998. pp.120-130. (1998).[
5] Tanaka, H., Asai, K., Ishikawa, M., and Konagaya, A. Hidden Markov Models and Iterative Alginers: Study of Their Equivalence and Possibilities. 1st Int. Conf. on Intelligent Systems for Molecular Biology. pp.395-401. (1993).[
6] http://genemark.biology.gatech.edu/GeneMark/[
7] Asai, K., Ueno, Y., and Yada, T. Recognition of Human Genes by Stochastic Parsing. Pacific Symposium on Biocomputing. (1998).[
8] 矢田他. DNA配列のモチーフパターンを表現する隠れマルコフモデルの生成. 情報処理学会論文誌 Vol. 37 No.6 (1996).[
9] Grate, L. et al. RNA Modeling Using Gibbs Sampling and Stochastic Context Free Grammars. 2nd Int. Conf. on Intelligent Systems for Molecular Biology. pp.138-146. (1994).[
10] Searls, D.B. The Computational Linguistics of Biological Sequences. In Artificial Intelligence and Molecular Biology. AAAI Press. pp.47-120. (1993).[
11] http://PredictionCenter.llnl.gov/casp3/Casp3.html[
12] 斎藤他. 分子動力学法プログラムAMBERとBarnes-Hut tree codeの並列化による高速化. 並列処理シンポジウムJSPP'98. pp.231-238. (1998).[
13] 鬼塚他. 多次元分布の線形基底変換による圧縮表現の提案、及びタンパク質残基間相対位置分布への応用. 第21回 情報処理学会 数理モデル化と問題解決研究会. pp.37-42.(1998).[
14] Matsuo, Y. A Systematic Analysis of Protein Folding Patterns. Master thesis, Department of Biophysics, Kyoto U. (1990).[
15] http://www.motif.genome.ad.jp/[
16] Asai, K., Yada, T., and Itou, K. Finding Genes by Hidden Markov Models with a Protein Motif Dictionary. Genome Informatics 1996. pp.88-97. (1996).[
17] Akutsu, T. Protein Structure Alignment Using a Graph Matching Technique. Genome Informatics 1995. pp.1-8. (1995).[
18] http://bio.ics.kagoshima-u.ac.jp/~masatom/researchj.html[
19] http://www.protein.osaka-u.ac.jp/csd/koshu.html[
20] http://www.immd.co.jp/programs/programs-j.html[
21] http://www.genome.ad.jp/kegg/[
22] Tanaka, H. Protein Function Database as a Deductive and Object-Oriented Database. Database and Expert Systems Applications 1991. pp.481-486. (1991).[
23] Weiss, S. and Indurkhya, N. Predictive Data Mining. Morgan Kaufmann. (1998). 24] http://www.e-cell.org/