Examples

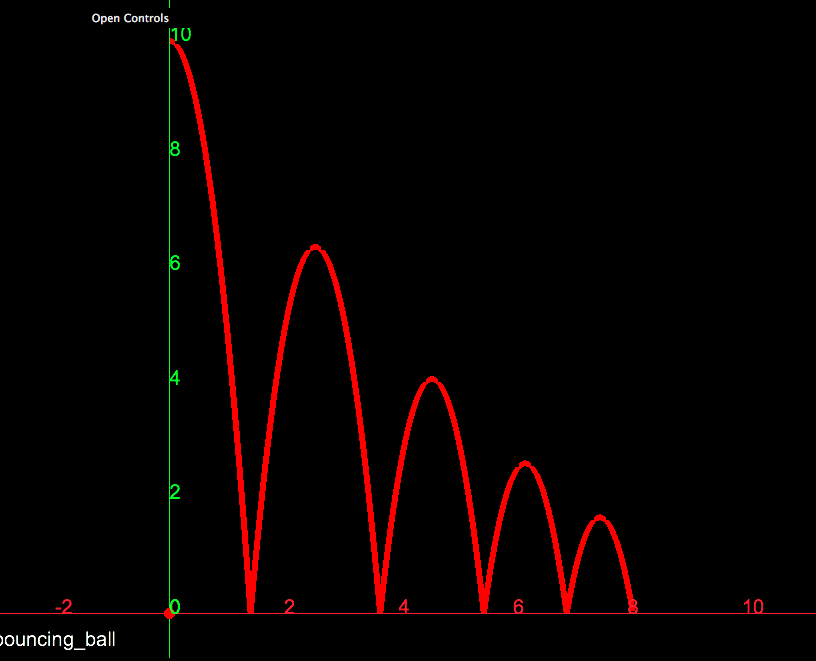
Bouncing particle †

// y stands for the height of the ball
INIT   <=> y = 10 & y' = 0. // initial state
FALL   <=> [](y'' = -10).   // falling
BOUNCE <=> [](y- = 0 => y' = -4/5*y'-).
                          // if the ball reaches the ground, it bounces
INIT, FALL << BOUNCE.     // FALL is weaker than BOUNCE

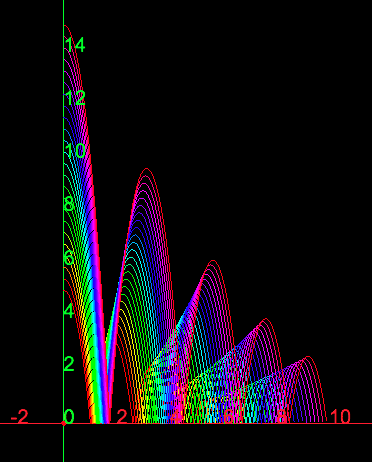
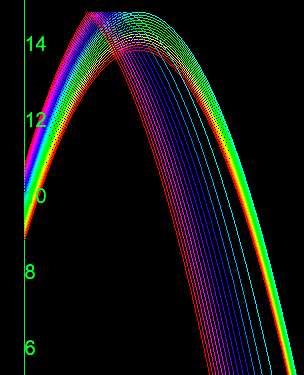
Bouncing_Particle.png

↑

Bouncing particle with a parametric initial height †

INIT   <=> 5 < y < 15 & y' = 0. // the initial height is uncertain
FALL   <=> [](y'' = -10).
BOUNCE <=> [](y- = 0 => y' = -4/5 * y'-).

INIT, FALL << BOUNCE.

Bouncing_Particle_with_a_Parameter.png

↑

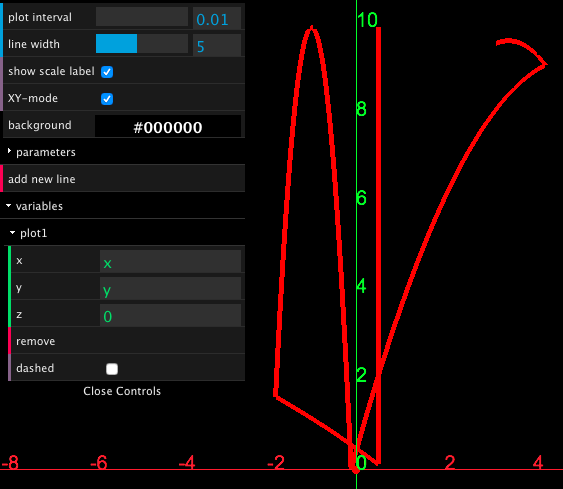
Bouncing particle in a parabolic vase †

/**
 *  bouncing particle on a curve of f(x) = (1/2) * x^2
 */

INIT <=> x = 1/2 & y = 10 & x' = 0 & y' = 0 & [](k = 1).
A    <=> [](x'' = 0 & y'' = -98/10).
/**
 *     sin = f'(x) / (1+f'(x))^(1/2)
 *     cos =     1 / (1+f'(x))^(1/2)
 *  new x' = (-k * sin^2 + cos^2) * x' + (k+1) * sin * cos      * y'
 *  new y' = (k+1) * sin * cos    * x' + (sin^2 + (-k) * cos^2) * y'
 */

SC <=> [](s = (x-)/(1+(x-)^2)^(1/2)
        & c = 1   /(1+(x-)^2)^(1/2)).

BOUNCE <=> [](y- = (1/2) * (x-)^2 => 
                x' = ( (-k) * s^2 + c^2 ) * x'- + ( (k+1) * s * c ) * y'-
              & y' = ( (k+1) * s * c ) * x'- + ( s^2 + (-k) * c^2 ) * y'- ).

INIT, SC, A << BOUNCE.

Bouncing_Paticle_on_a_Curve.png

↑

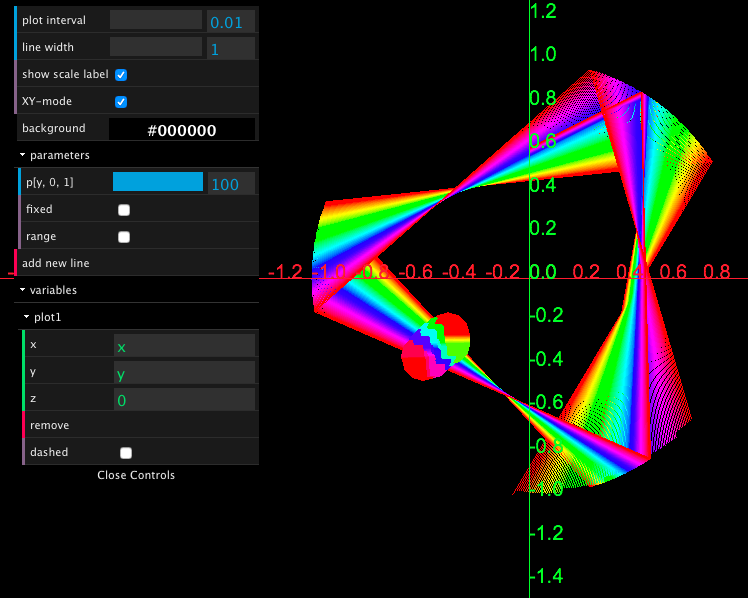
Bouncing particle in a circle †

INIT   <=> x = 0 /\ 0.5 < y < 0.6 /\ x' = 2 /\ y' = 1.
                                      // the initial position is uncertain
RUN    <=> [](x'' = 0 /\ y'' = 0).
BOUNCE <=> []((x-)^2 + (y-)^2 = 1 => 
                  x' = x'- - (x- * x'- + y- * y'-) * 2 * (x-)
               /\ y' = y'- - (x- * x'- + y- * y'-) * 2 * (y-)
).
INIT, RUN<<BOUNCE.

Bouncing_Particle_in_a_Circle.png

↑

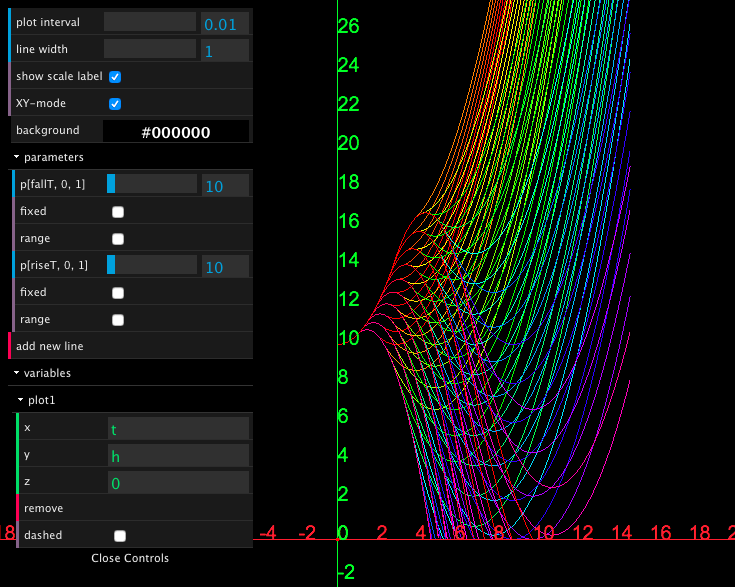
Hot-Air Balloon with multiple parameters †

/* A program for a hot-air balloon that repeats rising and falling */
// The initial condition of the balloon and the timer
// h: height of the balloon
// timer: timer variable to repeat rising and falling
INIT <=> h = 10 /\ h' = 0 /\ timer = 0.

// parameters 
// duration: duration of falling 
// riseT: duration of rising 
PARAM<=> 1 < fallT < 4 /\ 1 < riseT < 3  
                       /\ [](riseT' = 0 /\ fallT' = 0). 

// increasing of timer 
TIMER <=> [](timer' = 1). 

// rising of the balloon
RISE <=> [](timer- < riseT =>h'' = 1).

// falling of the balloon
FALL <=> [](timer- >= riseT => h'' = -2).

// reset the timer to repeat rising and falling
RESET <=> [](timer- >= riseT + fallT => timer=0).

// assertion for bounded model checking
ASSERT(h > 0).

// constraint hierarchies
INIT, PARAM, FALL, RISE, TIMER<<RESET.

Hot-Air_Balloon.png

↑

Bouncing particle with magnetic force †

INIT <=> y=10 & y'=0 & mag=0 & timer=0.
FALL <=> [](y''=-10+mag).
BOUNCE <=> [](y-=0=>y'=-y'-).
TRUE <=> [](1=1).
TIMER <=> [](mag'=0&timer'=1).
SWITCHON  <=> [](timer-=1=>mag=12&timer=0).
               // The magnetic force may be switched on at every one second
SWITCHOFF <=> [](timer-=1=>mag=0&timer=0).
               // The magnetic force may be switched off at every one second

INIT,TIMER<<(SWITCHOFF,SWITCHON)<<TRUE,FALL<<BOUNCE.

Bouncing_Particle_with_Magnetic_Force.png

↑

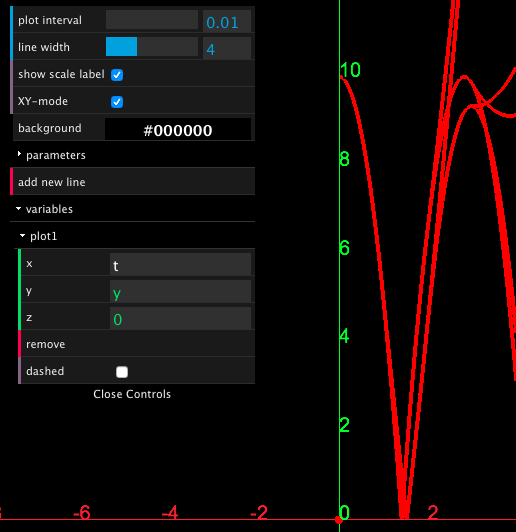
Bouncing particle thrown toward a ceiling †

INIT  <=> 9 < y < 11 & y' = 10. 
FALL  <=> [](y'' = -10).
BOUNCE <=> [](y- = 15 => y' = -(4/5)*y'-).

INIT, FALL << BOUNCE.
  • In this program, the trajectories change qualitatively dependent on the initial height \( y_0 \).
    • If \( 9 < y_0 < 10 \), the ball doesn't reach the ceiling.
    • If \( y_0 = 10 \), the ball touches the ceiling, but the velocity remains continuous.
    • If \( 10 < y_0 < 11 \), the ball bounces on the ceiling.
  • HyLaGI performs such a case analysis automatically.
    Bouncing_Particle_thrown_toward a_ceiling.png
Last-modified: 2017-03-17 (Fri) 08:42:45 (3168d)