Epsilon mode

Epsilon modeとは †

微小値を扱うシミュレーションのモードとなる
微小値(HydLaプログラム中ではパラメータ"eps"となる)を利用し, 特殊な処理を行う
- 微小値の高次項を削減する
- 高次項を削減したことによる影響を軽減する
- 不適切な場合分けを削減する
- 微小値の極限を求める
- 微小値による値の変化量(実際の値との差分)を求める
- HydLaプログラム中で扱える微小値は一つである("eps")
モデルの振る舞いを解析する際に利用可能である
- 特に, 誤差解析・感度解析等に有効となる

利用法 †

Hyrose実行時にオプションで指定する (-e [arg], --epsilon [arg])
- 引数は高次項の削減において行う線形近似の近似次数(例: -e1 => 一次近似, -e2 => 二次近似)
- ただし, 引数が0のときは近似は行わない(例: -e0)
あらかじめ微小値となるパラメータ(eps)を用いて, HydLaプログラムを記述する

高次項の削減 †

各フェイズの実行において, 各変数の値に現れる微小値(eps)の高次項を削減する
微小値の高次項を削減することで, 数式の複雑化を軽減できる
記号実行(パラメータ実行)で数式が複雑化してしまい解けない例題でも効果がある
高次項の削減にはn次近似を行う

問題点 †

高次項の削減により, 誤差が発生する
誤差の影響で解軌道が異なる場合がある
- 解軌道とは, 処理系Hyroseによって求まるモデル(HydLaプログラム)の振る舞いのこと
高次項の削減による解軌道が異なってしまう問題を解決する必要がある

現在の解決法 †

誤差の影響によって解軌道が異なる場合では, 次の条件による離散変化が考えられる
- 次の離散変化時刻までが微小な時間である
- 同じガード条件が離散変化の原因となる
現状, このような意図しない離散変化を無視することによって解軌道が変化しないようにしている

例題 †

このアルゴリズムでの例題のシミュレーションは次のようになる

円の内部を跳ねる質点の例題 †

INIT <=> x = eps & y = 4/5 & x' = 4 & y' = -1.

RUN <=> [](x" = 0 & y" = 0).

EPS <=> 0 < eps < 1/100 & [](eps'=0).

BOUNCE <=> []((x-)^2 + (y-)^2 = 1 =>

x' = x'- - (x- * x'- + y- * y'-) * 2 * (x-) &

y' = y'- - (x- * x'- + y- * y'-) * 2 * (y-)).

INIT, EPS, RUN << BOUNCE.

ボールの位置は, xy座標で示される
ボールは, 半径1で原点中心の円の円周に衝突する
円の内部は等速運動をする連続変化で, 円周との衝突は跳ね返る離散変化となる
ボールの初期位置のx座標に微小値が存在する
これはボールが円周に衝突する度に, 微小値(eps)の項の次数が一つずつ増えて複雑になっていく例題となる
- それぞれ数式に現れる微小値の項の最大の次数は
- PP1 : eps -> PP3 : eps^2 -> PP5 : eps^3 -> ....
この例題において, 初期値が円の内部ならば常に円の内部を運動していくはずである
しかし, 高次項を削減することにより円のそとにボールが飛び出してしまう
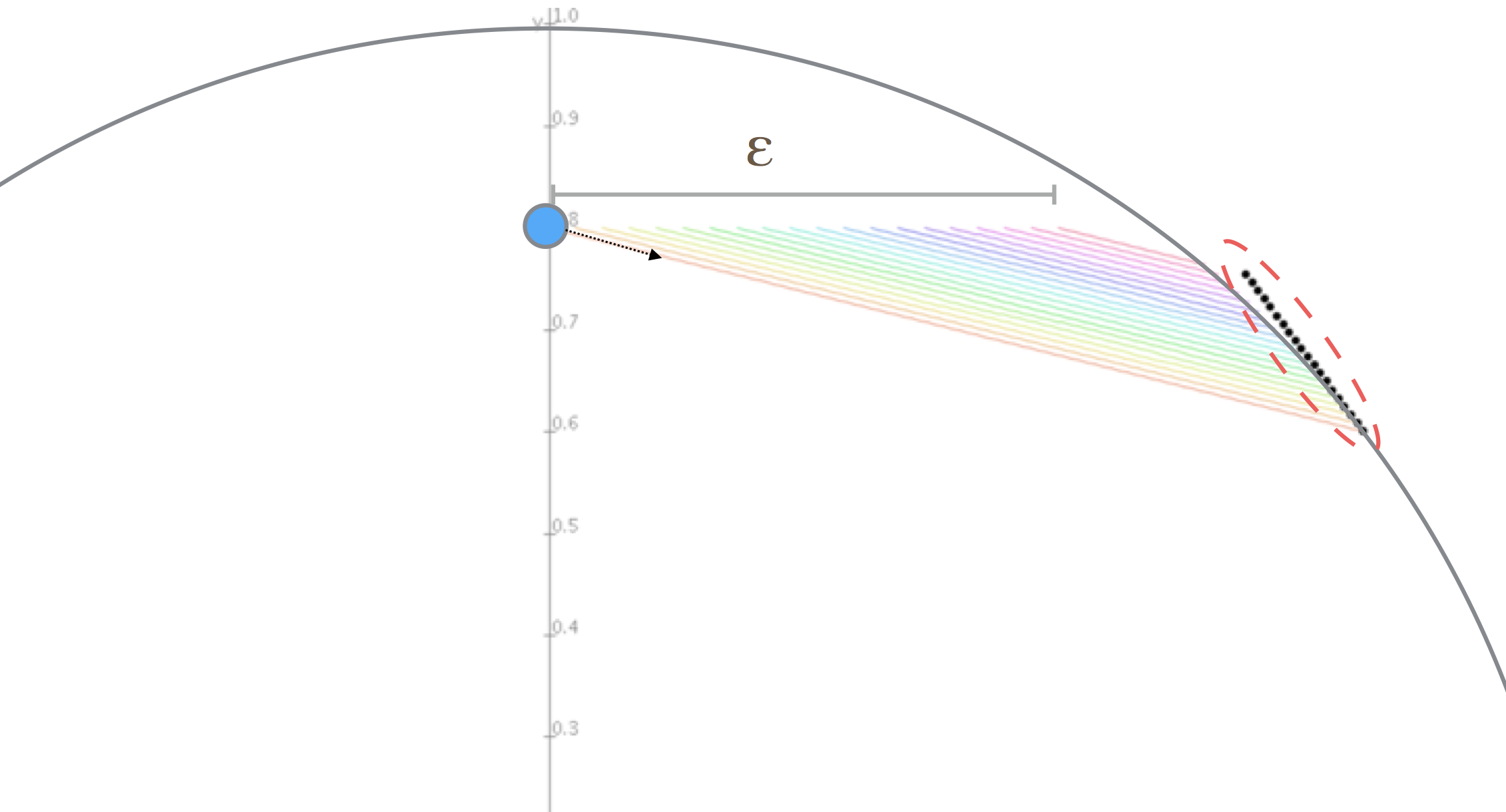
このようになり, 通常のシミュレーションならその後すぐに円周にぶつかって外側に飛んでいってしまう
そこで, 現在の解決法によって本来の解軌道と同様に円の内部へと運動するようになっている
高次項削減の効果として, シミュレーションにかかる時間が次のように削減される
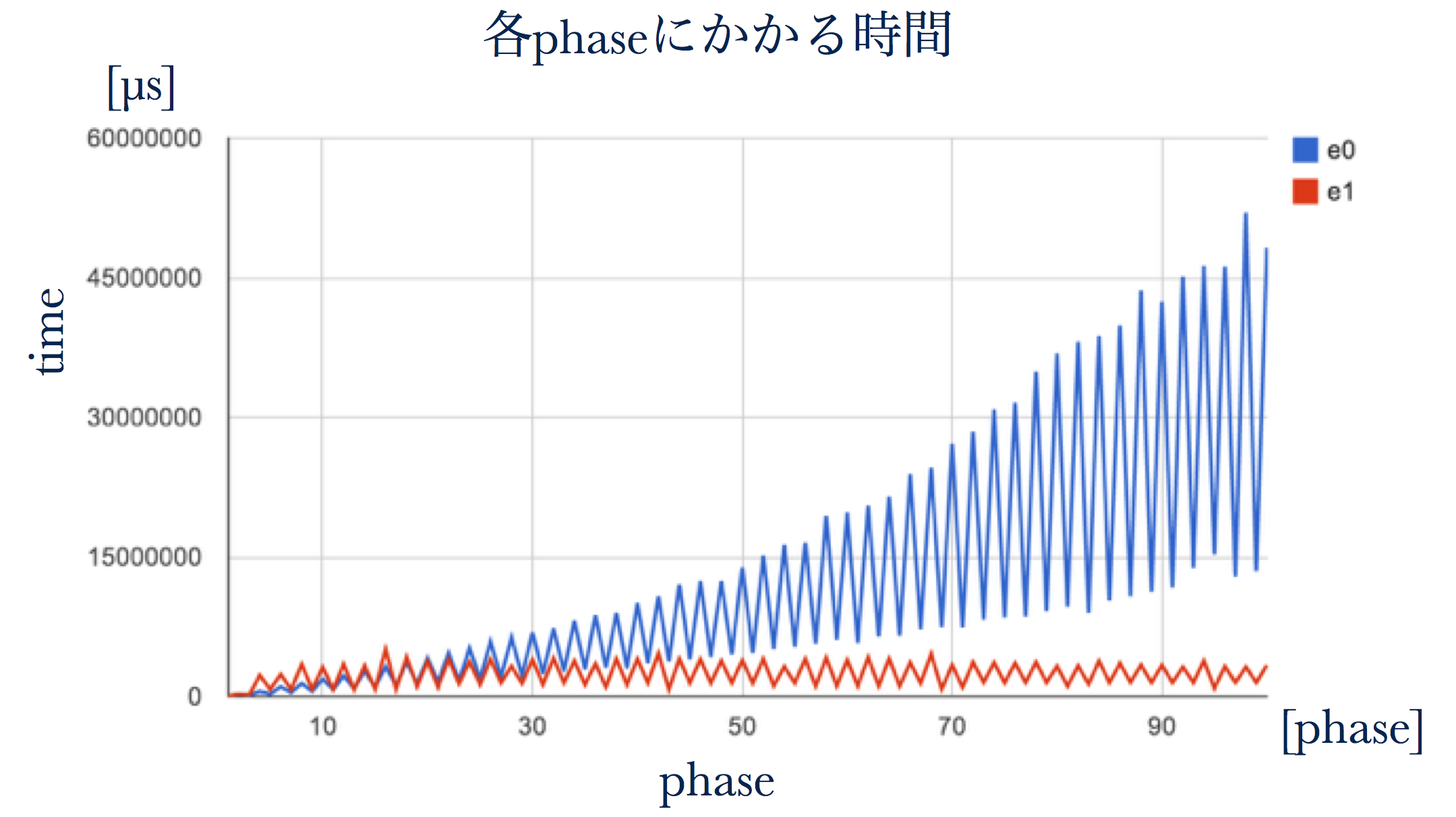
- e0は近似を行わない場合で, e1は一次近似を行う場合となる
高次項の削減により, 一次近似では微小値の項の次数が一次までとなるためシミュレーション時間が大きくなっていかない
高次項を削減しない場合では, 衝突ごとに一次ずつ微小値の最大次数が増えていき複雑化していくためシミュレーション時間が大きくなっていく

Attach file:

circle_time.png 1127 download [Information]

circle_problem.png 1011 download [Information]

Last-modified: 2017-03-02 (Thu) 03:21:30 (2612d)